Группа участников возле экспериментальной установки с дифрактометром POLI на реакторе FRM II. Слева направо: Эрл Бэбкок, Захир Салхи, Данияр Бериков, Алексей Гагарский, Вадим Новицкий, Юрий Копач.

Ядра, равновесная форма которых в основном состоянии отличается от сферически-симметричной называются деформированными. Деформированное ядро с отличным от нуля спином вращается, и если оно поляризовано, то возникает ось вращения z. Ось деформации ядра (ось симметрии) вращается вокруг оси z, причем плоскость вращения может составлять некоторый угол с осью z.

В седловой точке деформированное ядро описывается волновой функцией волчка D_JМК. Хорошие квантовые числа — это J, M и K, где J — полный момент деформированного ядра, M — его проекция на фиксированную ось z в пространстве, а K — проекция J на ось деления (рис. 1). Обычно предполагается, что не только J, но и компонент K сохраняется от седла до разрыва.

Рис. 1. Классическое разложение полного углового момента J на составляющие K вдоль оси деформации (оси деления) и R, перпендикулярные этой оси. Проекция J на фиксированную ось z в пространстве — это M

При делении такого вращающегося ядра осколки деления приобретают тангенциальную составляющую скорости в начальный момент разрыва шейки, направленной перпендикулярно оси деформации делящегося ядра. Таким образом, траектория осколка вместо прямолинейной, обусловленной кулоновским отталкиванием осколков, становиться гиперболической. Следовательно, ось вылета осколков деления на бесконечность будет не совпадать с осью деформации делящегося ядра в момент разрыва шейки, а отклоняться от нее на некоторый малый угол δ. Измерение данного угла дает представление о скорости вращения ядра.

В эксперименте регистрируется направление вылета осколка деления из мишени. Однако неизвестным остается ориентация оси деформации в момент разрыва шейки. Для ее определения требуется некая метка, характеризующая эту ориентацию. Такой меткой могут служить угловые распределения частиц, сопровождающие акт деления, поскольку они сформированы относительно оси деформации ядра в момент разрыва. Важно, чтобы их угловые распределения были анизотропными относительно оси деформации.

Эффект вращения ядра, так называемый ROT-эффект, впервые был обнаружен в угловых распределениях α-частиц тройного деления ядра ²³⁵U холодными поляризованными нейтронами [1]. Однако, траектории движения α-частиц тройного деления, образующихся в момент разрыва ядра, частично поворачиваются вместе с осью деления, поскольку на их движение существенно влияет кулоновское поле разлетающихся осколков (рис. 2). Поэтому для определения угла поворота именно оси деления (величина ROT-эффекта) в тройном делении необходимы детальные траекторные расчеты [2].

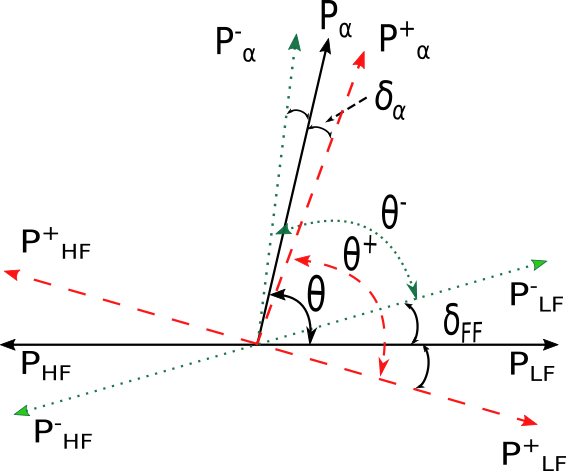
Рис. 2. Схематическое изображение формирования сдвига углового распределения α-частиц тройного деления. PLF, PHF – начальные направления легкого и тяжелого фрагментов соответственно; Pα — движение α-частицы в момент разрыва. «+» и «-» обозначают конечные направления объекта для противоположных направлений поляризации нейтрона

В качестве метки ориентации оси деформации перед развалом ядра могут служить так называемые “мгновенные” γ-кванты, испускаемые возбужденными осколками деления. Поиск и детальное исследование ROT-эффекта для мгновенных γ-квантов при бинарном делении ядер ²³³U и ²³⁵U впервые было проведено авторами [3-5]. Объяснение того, каким образом γ-кванты, эмитируемые не в момент разрыва шейки, а возбужденными осколками деления могут проявить ROT-эффект, было предложено В. В. Новицким [3], используя гипотезу В.М. Струтинского [6] о выстраивании спинов осколков деления в плоскости, ортогональной оси деления. Согласно данной модели, в момент разрыва шейки делящегося ядра, спины возбужденных осколков деления оказываются выстроены в плоскости, ортогональной оси, соединяющий центры масс двух осколков (далее «ось деформации»), и их ориентация не изменяются при отклонении траектории осколков от первоначального направления оси деформации (рис. 3). Описанная выше ориентация спинов осколков объясняет, в частности, и анизотропию испускания γ-квантов в делении относительно оси разлета осколков.

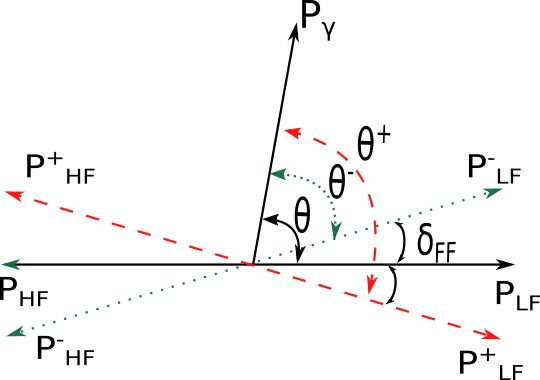
Рис. 3. Схематическое изображение формирования сдвига углового распределения мгновенных γ-квантов от осколков деления. P γ — движение γ-кванта в момент разрыва. «+» и «-» обозначают конечные направления объекта для противоположных направлений поляризации нейтрона

В эксперименте, когда детектор осколков и γ-квантов расположены в плоскости, ортогональной направлению пучка продольно поляризованных нейтронов, это проявляется как асимметрия счета совпадений сигналов с детекторов γ-квантов и детекторов осколков относительно направления поляризации пучка нейтронов. Асимметрия счета совпадений определяется отношением:

                                      (1)

здесь N⁺(θ) и N⁻(θ) – количество совпадений сигналов с детекторов γ-квантов и с детекторов осколков, расположенный под углом θ друг к другу в плоскости ортогональной оси продольно-поляризованного пучка нейтронов, измеренный при двух противоположных направлениях поляризации пучка нейтронов (рис. 4).

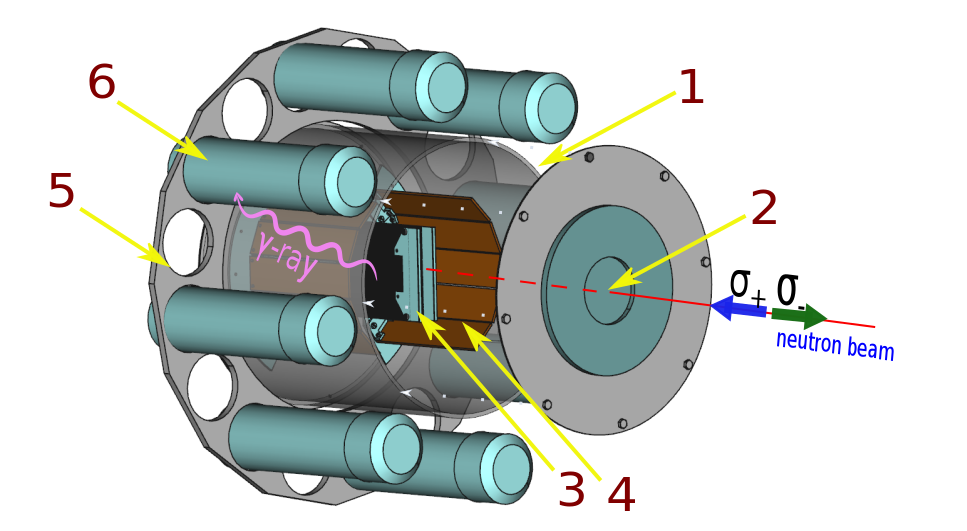
Рис. 4. Схема детекторной части экспериментальной установки. 1 — камера деления, 2 — входное Al окно камеры, 3, 4 — детекторы осколков деления на основе позиционно-чувствительных многопроволочных пропорциональных счетчиков низкого давления (стартовые и стоповые детекторы), 5 — держатель, 6 — сцинтилляционные пластиковые детекторы γ-квантов и нейтронов. Делящаяся мишень находится в центре, между стартовых детекторов

Очевидно, что

                                                  (2)

где F(θ) – функция, описывающая угловое распределение γ-квантов, а F'(θ) её производная в среднем положении детектора γ-квантов, расположенного под углом θ, δ — угол смещения оси деления. Таким образом, измеряя асимметрию и определяя функцию углового распределения γ-квантов, можно определить угол, на который смещается траектория осколка, а, следовательно, и угловую скорость, и направление вращения делящегося ядра. Важно заметить, что для γ-квантов, в отличие от α-частиц, определение угла поворота не требует траекторных расчетов и является в этом смысле модельно-независимым.

Согласно модели, предложенной в [3, 7], угол поворота делящегося ядра, в свою очередь, зависит от квантовых чисел J и K (величина углового момента и его проекция на ось деформации делящегося ядра соответственно), которые характеризуют каналы деления. При захвате ядром мишени со спином I s-волнового нейтрона (орбитальный момент равный 0) образуется компаунд-ядро в состоянии со спином  и в состоянии со спином . При этом соответствующая поляризация компаунд-ядра получается равной:

                                   (3)

где p_n- степень поляризации нейтронного пучка. Ядра со спинами переходных состояний J^± = (I ± 1/2) имеет разную скорость и направление вращения [8], т.е. знак угла поворота δ оси деления будет противоположным для разных состояний (см. 4).

                     (4)

где ω - угловая скорость вращения, K - проекция момента импульса на ось деления, ℑ - момент инерции делящегося ядра.

В области малых энергий нейтронов каналы деления смешиваются, т.е. в сечение деления вносят вклад оба резонанса, но с неопределённым соотношением вкладов в сечение деления обоих спиновых состояний компаунд-ядра. Для смеси состояний и  измеряется усредненное значение асимметрии:

                                                            (5)

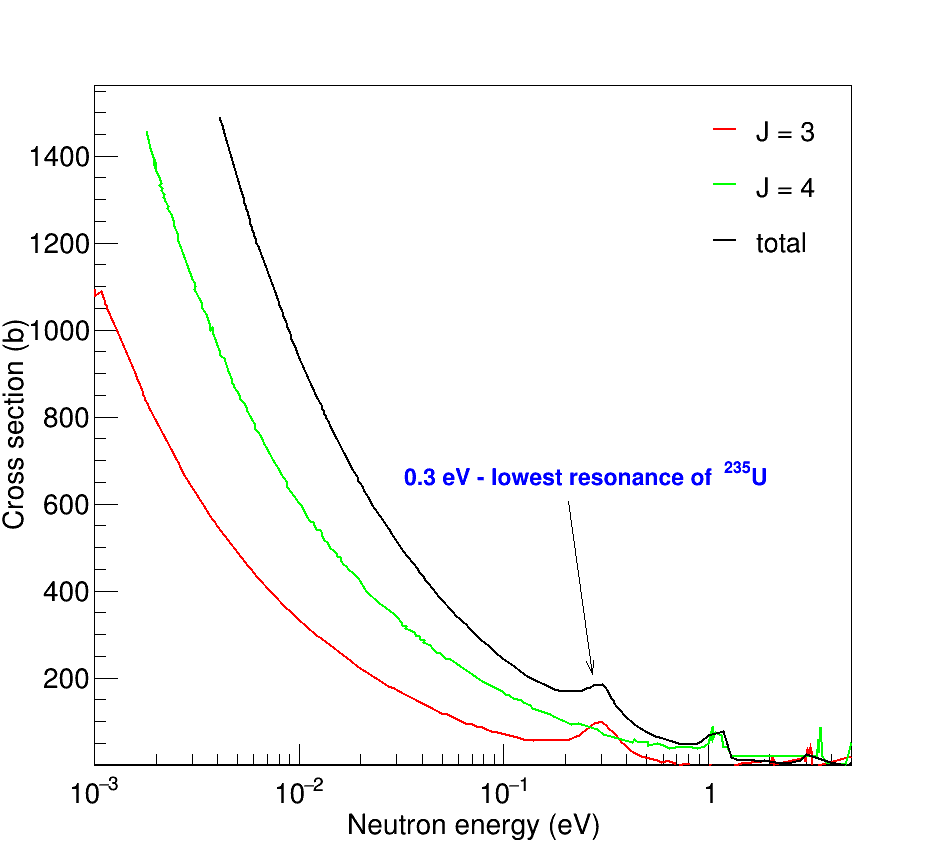
Отсюда следует, что необходимы измерения эффектов в резонансах. Анализ их физической природы будут более достоверным, что позволят получить данные о весах каналов J и K. Для таких исследований и выбран изотоп ²³⁵U, который имеет резонанс 3^- с энергией 0.3 эВ и резонанс 4⁺ с энергией 1.14 эВ (рис. 5).

Рис. 5. Спиново-разделённые сечения деления для 236U*. Красная линия соответствует спину J = 3, Зеленая линия соответствует спину J = 4, черная линия соответствует полному сечению

В 2018 г. впервые удалось провести измерение ROT-эффекта для гамма-квантов в делении ²³⁵U в низколежащем резонансе 0.3 эВ. Полученные результаты согласуются с теорией, однако для дальнейшего изучения квантово-механических свойств процесса деления целесообразно продолжение этих работ с целью получения данных для более высоколежащих резонансов, а также для других ядер. В частности, в качестве кандидатов было предложены ядра ²⁴¹Am и ²⁴⁵Cm [9].

Такие эксперименты могут быть начаты на пучке поляризованных нейтронов реактора ИБР-2. Несмотря на большую длительность импульсов реактора, разрешающая способность времяпролетной методики позволяет на пролетных базах порядка 15-30 м разрешать низколежащие резонансы до нескольких электронвольт. Дальнейшие работы могут быть продолжены на внешних источниках нейтронов, таких как nTOF (ЦЕРН) CSNS (Китай) или ESS (Швеция).

ЛИТЕРАТУРА

1. F. Goennenwein, M. Mutterer, A. Gagarski, I. Guseva, G. Petrov, V. Sokolov, T. Zavarukhina, Yu. Gusev, J.von Kalben, V. Nesvizhevski, T. Soldner, Phys. Lett. B 652, 13 (2007);
2. I.S. Guseva, Yu.I. Gusev, Bull. Russ. Acad. Sci. Phys. 71, 367 (2007);
3. G.V. Danilyan, J. Klenke, V.A. Krakhotin, V.L. Kuznetsov, V.V.Novitsky, V.S.Pavlov, P.B.Shatalov, Phys. At. Nucl.72, 1812 (2009);
4. G.V. Danilyan, J. Klenke, V.A. Krakhotin, Yu.N. Kopach, V.V.Novitsky, V.S.Pavlov, P.B.Shatalov, Phys. At. Nucl.74, 671 (2011);
5. G.V. Danilyan, J. Klenke, Yu. Kopatch, V.A. Krakhotin, V.V. Novitsky, V.S. Pavlov, P.B. Shatalov, Phys. At. Nucl. 77, 677 (2014);
6. Струтинский В. М. Об угловой анизотропии γ-квантов, сопровождающих деление // ЖЭТФ. – 1959. – Т. 37. – С. 861-863;
7. G.V. Valsky, A.M. Gagarski, I.S. Guseva, D.O. Krinitsin, G.A. Petrov, Yu.S. Pleva, V.E. Sokolov, V.I. Petrova, T.A. Zavarukhina, and T.E. Kuzmina, Bull. Russ. Acad. Sci. Phys. 74, 767 (2010);
8. A.M. Gagarski, I.S. Guseva, F. Goennenwein, Yu.N. Kopach, M. Mutterer, T.E. Kuz’mina, G.A. Petrov, G. Tyurin, V. Nesvizhevsky, Cryst. Reports 56, 1238 (2011);
9. I. Guseva, Yu. Gusev, Nucl.Phys.A 1030 (2023) 122592.